For
me, a physicist, the simplicity of physics is its beauty. For example,
when we want to describe the motion of all objects, on earth or in
heaven, we simply use Newton’s three laws of motion only + the law of gravity.
For me it’s as beautiful as the fact that to explain so many geomtric
facts , we only need just six axioms. The beauty of this geometry in
junior high I get when axiomatic geometry is still taught as a
subject.In the 19th century when George Boole 
finally formulate logic as an algebra based on a very simple arithmetic
based only two numbers, 0 and 1. With this new formulation, the verbal
Aristotelian syllogism in logic is merely a special case of logical
tautology. But I still wonder: how many are the axioms of logic algebra.
finally formulate logic as an algebra based on a very simple arithmetic
based only two numbers, 0 and 1. With this new formulation, the verbal
Aristotelian syllogism in logic is merely a special case of logical
tautology. But I still wonder: how many are the axioms of logic algebra.
The problem is, what is the axiom basis of logic and how many? The
formal foundations of mathematics are called axioms. For example,
Euclidean geometry is built on the basis of just six axioms. That is why
in the past, when I was a university student, when I learn that the
propositional calculus of Whitehead 
-Russell 
,
in his Principia Mathematica , built on five axioms and one rule of
inference, I was so amazed. However, it turns out that my admiration is
nothing. It is just the first step on the way to the highest admiration
in the end phase of may journey to Boolean space as a part of the
Platonic space of ideas.
When I became a lecturer in the 70s of last century, in the British Council library of Bandung, I found a book called “Laws of Form”, written by George Spencer Brown
, Which was praised by Bertrand Russell as the greatest discovery in
the field of mathematics, I was very interested. But then I am very
disappointed, because I can not understand the strange formulas listed
in the book. Unfortunately, later on, the book was missing from the
library book shelves so that I could never read it again.
Fortunately, I was connected to the internet in 2000, when I was retired. In the internet, I found an electronic book titled “Laws of Form” by Louis Kauffman
. From it, I know that the strange formulas in the Spencer-Brown book
of the 70s actually are the algebraic equations in the Boolean logic in
an unconventional notation. Later on, I reformulated Brownian algebra in
a box algebra with colored balls: Objective primary algebra
I was so excited to know the fact that Spencer-Brown managed to cut
the number of axioms of Russell-Whitehead to just two. For me, this
means that mathematical logic is much more beautiful than geometry. This
fact truly amazed me, because the Boolean algebra of logic is only
based on a pair of axioms. At the end of this article I’ll show you that
the basic axioms of algebraic logic is not two, but one that is 1.
Please follow my journey towards this ultimate truth.
Within the framework of a disjunctive meaning, as adopted Spencer-Brown, the juxtaposition of two letters, which represent the two statements, considered as a merger of the two by OR. Within the framework of conjunction, as it is embraced by Charles Sanders Peirce, the juxtaposition was read as merging two statements by AND. If we merge disjunctively, VOID is read as a symbol for FALSE, while the incorporation of conjunctive merge, VOID is the epitome of TRUE.
When I read the single axiom Kauffman conjunctively, I immediately noticed that the single axiom is actually none other than the mathematical expression of an ancient principle, pre-Aristotle , Contradictio ad Absurdum . The principle states that a statement is true if and only if the denial contradictory. It is very intuitive, because the principle that means: A IS TRUE IF AND ONLY IF NOT A IS FALSE.
You can imagine how happy I was, when it discovered that modern algebra Boolean logic it turns out to be founded on an ancient logic principle has been known long before Aristotle formulated the science of logic. This fact shows that the basic logic is only one and this one turned out to be very intuitive. For me this is ultimately showing the beauty of simplicity of logic. Read Ultimate Simplicity of Logic
Spencer-Brown even stated that the whole 24 varieties of valid syllogism can be proved in the same way. I do not know, what are the 24 varieties of valid syllogism. Fortunately, I finally found that out in an Wikipedia article about the syllogism. Over the years I unsuccessfully tried to prove that Brown’s statement. For that, fortunately, I was helped by a pictorial notation Kauffman symbolizing NOT operation with confinement in a BOX.
For ease of visualization. I replace the letters in algebra Box Kauffman with colorful balls. The new pictorial Algebra I call the object logic. Thanks God, by reading the box algebra of Kauffman as a game drawing and erasing pictures, finally I can attest to the validity of the 24 Aristotelian-Leibniz syllogism.
Even at the end, I can attest to the 24 valid syllogism was equivalent to each other. The fact that I refer to as the unity of syllogistic this made me even happier. You see, I find out that it has not been disclosed by others throughout my search on the Internet eith Google search engine. I reported my findings in a series of blogs that I then united in a ebook: Syllogistic Unity. Read Syllogistic unity
Discovery the greater tautological unity is, in fact, very surprising to me. You see, every system is axiomatic algebraic logic is complete as it can prove all tautologies or existing logical truth. Remarkably, all the logic tautology, in fact, can be derived from the axioms by simply using algebraic substitution rules. That is the unity of tautological truth is algebraic or mathematical.
This tautological unity indicates that the validity of the syllogism as a tautology, can also be actually derived from the principle of Contradictio ad Absurdum. Here’s the proof: a syllogism is true, if and only if its denial is false.
Denial of a syllogism called by Christine Ladd-Franklin, Peirce’s student who later became the first female Doctor of the United States in the field of natural science, as antilogism. So a syllogism is valid if only if its antilogism is false. That is indeed a valid syllogism can be derived from a single axiom Kauffman: contradictio ad absurdum. This fact encouraging my heart.
Peirce proved this with his 5 rules of logical inference which may be
difficult to remember. I will prove it mathematically with the notation
of Boolean NOT(x) = 1 – x, x AND y = x -1 + y and IF x THEN y = x-> y = 1 – x + y as follows:
1 = (1-a) -1 + (1 + a) {because 1-1 = 0 and a-a = 0}
= (1-a-a + a) -1+ (1-a + a + a) {from a-a = 0}
= (a + a-> a) AND (a + a -> a) {from the definition of x-> y and x AND y}
= (a + a = a) {from the definition x = y}
= ((a + b) -1+ (a + 1-b ) = a) {because 1-1 = 0 and b-b = 0}
= ((1- (1-a) + b) -1+ (1- (1-a) +1 -b) = a) {because – (- a) = + a and 1-1 = 0}
= ((NOT(a) -> b) AND (NOT(a) -> NOT(b)) = a) {from the definition of x-> y and NO (x)}
= ((IF NOT(a) THEN b) AND (IF NOT(a) THEN NOT(b)) = a) {the translation of -> in words}
Because TRUE is 1, then the single axiom of Kauffman
(IF NOT(a) THEN b) AND (IF NOT(a) THEN NOT(b)) = a,
formulated in the Box Algebra of Kauffman as
[[a] b] [[a ] [b]] = a,
is TRUE.
Now, in my retirement, I am faced an extraordinary fact that the mental space, which is inhabited by our thoughts, is based on just one axiom: 1. This brought me an incomparable happiness because the universe is derived from the ABSOLUTE ONE in accordance to Tawheed, apparently of origin of the ideals is also a relative One. The relative One is just a shadow of the ABSOLUTE ONE. Allah Is The Greatest. Praise to the Lord of all the worlds.
OK, the lines above is modified reposting of my blog The Ultimate Unity of Logic
Discovering Arithmologic
It is subjectivelly religious since I am a muslim. However, further contemplation will also show that the ultimate foundation of logic is 0 (symbol of TRUE) in Peircean and Sommersian Arithmologic
The Ending: Combinatoric Game of Thing
Finally I simulated Sommersian arithmologic in the various combinatoric games of thing in series of blogs from Literal Combinatoric of Plouquet
to Holological Reflection
Thank you for following the trackback of my journey in logic.
Hopefully, you will join holologics@yahoogroups.com.
-Russell ,
in his Principia Mathematica , built on five axioms and one rule of
inference, I was so amazed. However, it turns out that my admiration is
nothing. It is just the first step on the way to the highest admiration
in the end phase of may journey to Boolean space as a part of the
Platonic space of ideas.When I became a lecturer in the 70s of last century, in the British Council library of Bandung, I found a book called “Laws of Form”, written by George Spencer Brown
, Which was praised by Bertrand Russell as the greatest discovery in
the field of mathematics, I was very interested. But then I am very
disappointed, because I can not understand the strange formulas listed
in the book. Unfortunately, later on, the book was missing from the
library book shelves so that I could never read it again.Fortunately, I was connected to the internet in 2000, when I was retired. In the internet, I found an electronic book titled “Laws of Form” by Louis Kauffman
. From it, I know that the strange formulas in the Spencer-Brown book
of the 70s actually are the algebraic equations in the Boolean logic in
an unconventional notation. Later on, I reformulated Brownian algebra in
a box algebra with colored balls: Objective primary algebra |
|||||
Axiomatic Unity of Logic
When I discovered that there is a double foundation logic space, I asked: is the beauty of the logic ended there? Praise God, the logic was much more beautiful. You see, I found out later, Louis Kauffman managed to cut the number of axioms of algebraic logic. It only took a single axiom. But unfortunately, the axiom that when I first read it is not intuitive. Thankfully, in his book, Kauffman stated that the formulas Brown strange it can be read by two different meanings framework: disjunctively and conjunctively.Within the framework of a disjunctive meaning, as adopted Spencer-Brown, the juxtaposition of two letters, which represent the two statements, considered as a merger of the two by OR. Within the framework of conjunction, as it is embraced by Charles Sanders Peirce, the juxtaposition was read as merging two statements by AND. If we merge disjunctively, VOID is read as a symbol for FALSE, while the incorporation of conjunctive merge, VOID is the epitome of TRUE.
When I read the single axiom Kauffman conjunctively, I immediately noticed that the single axiom is actually none other than the mathematical expression of an ancient principle, pre-Aristotle , Contradictio ad Absurdum . The principle states that a statement is true if and only if the denial contradictory. It is very intuitive, because the principle that means: A IS TRUE IF AND ONLY IF NOT A IS FALSE.
You can imagine how happy I was, when it discovered that modern algebra Boolean logic it turns out to be founded on an ancient logic principle has been known long before Aristotle formulated the science of logic. This fact shows that the basic logic is only one and this one turned out to be very intuitive. For me this is ultimately showing the beauty of simplicity of logic. Read Ultimate Simplicity of Logic
Ultimate Simplicity of Logic
Ultimate
Simplicity of Logic Armahedi Mahzar (c) 2011 Logic in history has many
formulations. The first formulation is verbal as it is formulated by
Aristotle , the…
|
|||||
The Syllogistic Unity
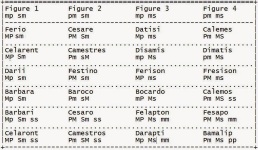
However, my happiness was tainted because I was unable to derive the Aristotelian syllogism from Boolean algebra. The explanation Boole in his famous book was “Laws of Thought” on Aristotelian syllogism proves how completely beyond my comprehension because it is so complex. However, in the appendix to the book “Laws of Form” Spencer Brown describes a simple prove of the validity of the Aristotelian syllogism Barbara from algebra by using his strange notation.Spencer-Brown even stated that the whole 24 varieties of valid syllogism can be proved in the same way. I do not know, what are the 24 varieties of valid syllogism. Fortunately, I finally found that out in an Wikipedia article about the syllogism. Over the years I unsuccessfully tried to prove that Brown’s statement. For that, fortunately, I was helped by a pictorial notation Kauffman symbolizing NOT operation with confinement in a BOX.
For ease of visualization. I replace the letters in algebra Box Kauffman with colorful balls. The new pictorial Algebra I call the object logic. Thanks God, by reading the box algebra of Kauffman as a game drawing and erasing pictures, finally I can attest to the validity of the 24 Aristotelian-Leibniz syllogism.
Even at the end, I can attest to the 24 valid syllogism was equivalent to each other. The fact that I refer to as the unity of syllogistic this made me even happier. You see, I find out that it has not been disclosed by others throughout my search on the Internet eith Google search engine. I reported my findings in a series of blogs that I then united in a ebook: Syllogistic Unity. Read Syllogistic unity
 |
Syllogistic unity
Proving the equivalence of all valid syllogism using pictorial formulation of Boolean agebra
|
||||
The Tautological Unity
However, the excitement does not last long, when then realized that it was trivial, because if a valid syllogism means he is equivalent to 1 or TRUE. Because everything is equivalent to one, then by itself all the valid syllogism equivalent to each other. However, this finding would indicate that all identities of Boolean logic or tautologies are actually equivalent to each other too. Because any valid syllogism is really just a tautology.Discovery the greater tautological unity is, in fact, very surprising to me. You see, every system is axiomatic algebraic logic is complete as it can prove all tautologies or existing logical truth. Remarkably, all the logic tautology, in fact, can be derived from the axioms by simply using algebraic substitution rules. That is the unity of tautological truth is algebraic or mathematical.
This tautological unity indicates that the validity of the syllogism as a tautology, can also be actually derived from the principle of Contradictio ad Absurdum. Here’s the proof: a syllogism is true, if and only if its denial is false.
Denial of a syllogism called by Christine Ladd-Franklin, Peirce’s student who later became the first female Doctor of the United States in the field of natural science, as antilogism. So a syllogism is valid if only if its antilogism is false. That is indeed a valid syllogism can be derived from a single axiom Kauffman: contradictio ad absurdum. This fact encouraging my heart.
The Foundation of the Unity: 1
However, starting from the reference of Kauffman, I finally found out that Charles Sanders Peirce actually built a system of logic, namely The simple existential graph system, based on just one axiom as well. However, his axiom is much simpler than the principle of Contradictio ad Absurdum in its formulaic form a IF AND ONLY IF (IF NOT a THEN b) AND (IF NOT A THEN NOT b). TRUE is his only axiom and it is denoted by ZERO in the system of existential graphs. The principle of Contradictio ad Absurdum, which is the single axiom of Kauffman, is just a theorem in Peirce’s Existential Graph axiom system. |
The simple existential graph system
simplification of the existential graph system of Charles Sanders Peirce
|
||||
1 = (1-a) -1 + (1 + a) {because 1-1 = 0 and a-a = 0}
= (1-a-a + a) -1+ (1-a + a + a) {from a-a = 0}
= (a + a-> a) AND (a + a -> a) {from the definition of x-> y and x AND y}
= (a + a = a) {from the definition x = y}
= ((a + b) -1+ (a + 1-b ) = a) {because 1-1 = 0 and b-b = 0}
= ((1- (1-a) + b) -1+ (1- (1-a) +1 -b) = a) {because – (- a) = + a and 1-1 = 0}
= ((NOT(a) -> b) AND (NOT(a) -> NOT(b)) = a) {from the definition of x-> y and NO (x)}
= ((IF NOT(a) THEN b) AND (IF NOT(a) THEN NOT(b)) = a) {the translation of -> in words}
Because TRUE is 1, then the single axiom of Kauffman
(IF NOT(a) THEN b) AND (IF NOT(a) THEN NOT(b)) = a,
formulated in the Box Algebra of Kauffman as
[[a] b] [[a ] [b]] = a,
is TRUE.
Conclusion and Aftermath:
If the Euclidean geometry requires 6 axioms, it turns out that the Boolean algebra necessitates only one single axiom axiom alone and it is 1 as it has been demonstrated above. Back then, after finising junior high school, I admired the beauty of Euclidean geometry that describes physical space, which is inhabited by the universe, that is based on 6 axioms.Now, in my retirement, I am faced an extraordinary fact that the mental space, which is inhabited by our thoughts, is based on just one axiom: 1. This brought me an incomparable happiness because the universe is derived from the ABSOLUTE ONE in accordance to Tawheed, apparently of origin of the ideals is also a relative One. The relative One is just a shadow of the ABSOLUTE ONE. Allah Is The Greatest. Praise to the Lord of all the worlds.
OK, the lines above is modified reposting of my blog The Ultimate Unity of Logic
| |
The Ultimate Unity of Logic
Ultimate
Unity of Logic: 1 is the Foundation Armahedi Mahzar (c) 2014 For me, a
physicist, the simplicity of physics is its beauty. For example, when we
want to …
|
||||
It is subjectivelly religious since I am a muslim. However, further contemplation will also show that the ultimate foundation of logic is 0 (symbol of TRUE) in Peircean and Sommersian Arithmologic
 |
Arithmologic
ARITHMOLOGIC
Armahedi Mahzar (c) 2015 George Spencer-Brown reduced logic algebra to
an axiomatic system based on just two axioms (contradiction…
|
||||
Finally I simulated Sommersian arithmologic in the various combinatoric games of thing in series of blogs from Literal Combinatoric of Plouquet
 |
Literal Combinatoric of Plouquet
Literal
Combinatoric of Plouquet Armahedi Mahzar (c) 2015 Gottfried Ploucquet
(1716-1790) In previous blog, I pointed out that there are three kinds
of arithmologi…
|
||||
 |
Holological Reflection
Holological
Reflection Armahedi Mahzar (c) 2015 In my previous blog, I was telling
you a my story of logic in a subjective perspective. In the end of the
story I in…
|
||||
Hopefully, you will join holologics@yahoogroups.com.
of the Yale university who created the WFF’N PROOF: a game of logic based on Polish notation.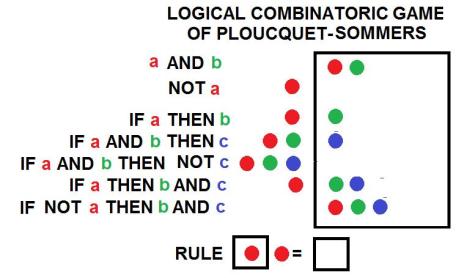
make another revolution when they represented any logical expressions
as diagrams in two dimensional space. Peirce used circles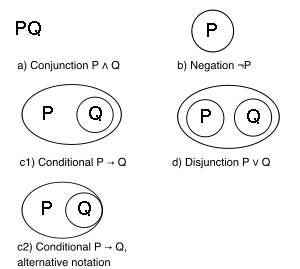 
and Gottlob Frege used trees 
. Later, George Spencer-Brown 
and Louis Kauffman 
as parts of their expressions of logical propositions. I will call such
method as pictologic as the concise term of pictorial logic.
Pictological revolution was following the electrical industrial
revolution.
. Calculating logic with objective algebra, I am inspired to replace
boxes and trees with real objects like cards and sticks to transform the
algebras of logic into games of thing 
. I will call my three dimensional method as hylologic as the concise
term for object logic. Hylological revolution is following informational
electronic revolution.
the discoverer of Venn
method used movable parts of wooden ellipses
created a logical piano 
to reason with syllogism. Allan Marquand
. Peirce transformed Marquand mechanical machine into an electromagnetic logical machine 
-Whitehead 
book Principia Mathematica. I read it, still I could not comprehend it.
. In this book I understood that the primary algebra in GSB book is nothing but a simplified axiomatization of Boolean algebra. But I am not interested in logic until I have found another logic operation XOR in the formulation of imaginary units of 16 dimensional number called sedenion.
