TheCombino
Magic Square
Armahedi Mahzar (c)2016
In my last blog we rearange nominos
into a magic square. No we will discuss the four-colored combinoes. A combino
card contains all possible combination of four colored dots. There are
exactly 16 four colored combinoes, if we include the empty combination.
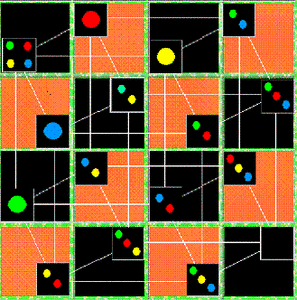
The following picture is a 4×4 checkerboard with each cell is containing a combino of 4 colors. The colors are red, blue, yellow and green.

The following picture is a 4×4 checkerboard with each cell is containing a combino of 4 colors. The colors are red, blue, yellow and green.
In it combinoes are placed randomly into each small square. So the numbers of colored dots in each column, row or diagonal are different.
Can we rearrange the combinoes to get the Combino Magic Square where each column, row and diagonal is containing exactly two of each colored dots?
In fact, if only you realize there is one to one correspondence between the combinoes and the varinoes. You can transform the Varino Magic Square

to the Combino Magic Square.
We can associate the four colored
squares in varino with the four possible ombinations of any two
colors in combino, and then you associate the four colored dots in
varino with the four possible combinations of the other two
colors in combino.
Let us associate
Red Square in varino with Empty combino,
Blue Square in varino with Red Dot in combino,
Green Square in varino with Blue Dot in combino and
Yellow Square in varino with combination of Red Blue Dots in combino
and I will associate
Red Dot in varino with Empty combino,
Blue Dot in varino with Yellow Dot in combino,
Green Dotin varino with Green Dot in combino and
Yellow Dot in varino with combination of Yellow Green Dots in combino.
Let us choose this associations to built as correspondence rule
I think this iss a good choice. With this choice, we can associate any varino with one combino by associating any varino with colored dot on colored square with the combination of combino colored dots associated to the varino colored dot and colored square into one combino.
Green Dot on Yellow Square varino is corresponded to
Green Red Blue Dots combino.
Another example is Blue Dot on Green Square varino is corresponded to
Yellow Green Dots combino.
We see that we can correspond the 16 combinoes to the 16 varinoes one by one.
After making the correspondence, you can transform the Greco-Latin Square
into Combino Magic Square like this one.
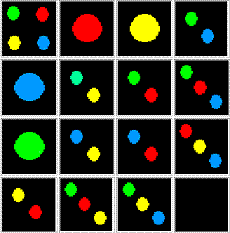
You’ve done it once more. But do you see that this Combino Magic Square is just a projection of a Combino Magic Hypercube 2x2x2x2. Magic hypercube in which each one of its faces is containing exactly two colored dots?
What I know is the projection of the four dimensional hypercube is like this
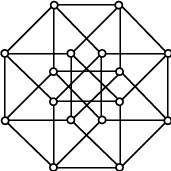
The wonderful fact is that we can catch it corners into the squares of 4×4
checkerboard
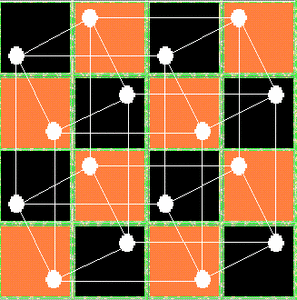
So, we will see there is the magic hypercube of combinoes