Peircean Chips Game of Logic

Peircean Chips Game of Logic
Armahedi Mahzar © 2015

 

In my previous blog I presented a simulation of Boolean arithmologic with a game of chips. In this blog I will show you how to simulate Peircean Arithmologic using the same chips. It will be shown that the derivation of the conclusion from two premises in the valid syllogisms is very easy. There are 24 valid syllogism as it is shown in the following Leibniz table:

Representing Logical Expression with Chips

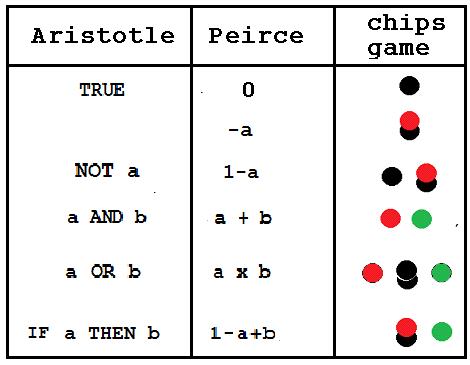
Aristotle using verbal string of words to represent logical expression such as IF a THEN b. George Boole in 19^th century used string of algebraic symbols to represent the mentioned logical expression as 1-a+b. In the 20^th century, George Spencer-Brown used a containment of forms 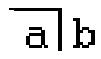   to express the same logical expression as . Later, Louis Kauffman in his Box Algebra represent the same logical expression as  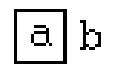. Finally, I replaced Kauffman letters with colored chips, to get Object Logic algebra the representation of the logical expression IF a THEN b is  .
Now, we can construct an arithmologic game that simulates Boolean arithmetic by representing TRUE or 1 by black chip and variables by colored chips. Other representations for logical expressions is shown in the following table

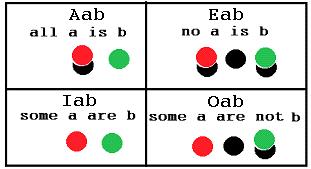
The Categorical Proposition of Aristoteles

If a is represented by RED chip, b by a GREEN chip and 1 by a BLACK chip, the the four fundamental categoric proposition of Aristotle can be represented as it is shown in the following table.

Simulating the Syllogism Validity Proof

Reasoning by syllogism now can be simulated by three steps algorithm

1. Combined all the representation of premises with AND as the combinator.
2. Dispose all chip pairs  where the red chip is the symbol of any colored chip.

3. Read the rest as conclusion. If the rest is containing two color chips then the syllogism is valid. Otherwise it is invalid.

Proving Valid Syllogisms

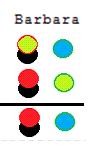
To prove the Barbara syllogism, IF all m is p AND all s is m THEN all s is p, we represent s, m and p with red, green and blue chips and represent the conjunction of premises as the chips configuration above the horizontal line in the picture below.

By discarding opposite pairs of chips, we will get the chips configuration below the line which can be read as the conclusion of the syllogism.

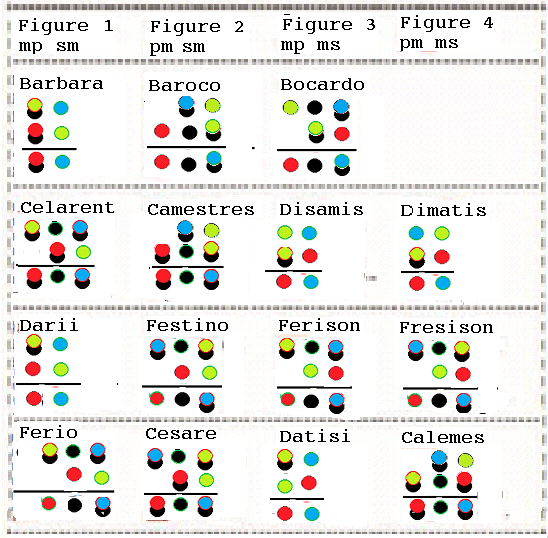
The proof the validity of all 15 syllogisms can be derived with the help of the following table.

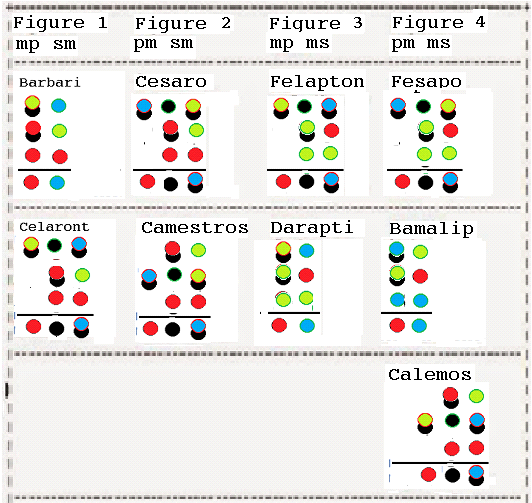
Beside the 15 valid syllogisms without any assumption of the existence of a certain term, there are 9 valid moods of syllogism containing existential assumption.

For example, the validity of Barbari syllogism which is containing one assumption of the existence of the subject term can be proven like this, where the the third proposition is Iss is represented by the following picture.

In the proof, we just eliminate the oppositional pair off chips above the horizontal line to get the chip configuration below the line.

The proof the validity of all 9 existential syllogisms can be shown in the following table.

Afternotes

The chips game can be used to prove hypothetical and disjunctive of the Stoic logician. In fact it can be used to prove any Boolean tautology. So it is shown that a game of concrete objects can simulate any logical proof in abstract algebraic symbols.

The objects chosen in this blog are colored chips. However the colored chips can be replaced with any objects and the black chips can be replaced with any sheets of paper. For example, the colored chips are replaced with colored marbles and the black chips are replaced with closed cards.

In this blog, logic is formulated with Peircean algebraic symbols. However logic can also be represented Sommersian arithmetical symbols. Both Peircean pictorial and Sommersian literal formulations can also be simulated with similar game of concrete things. The new games is simpler than the Boolean game described before.

All the logic games of concrete things are so easy to play that it can be taught to any kindergarten kid. Surely, we just teach them the rules of formation and transformation of the things arrangement without the logical interpretation.

Once they skilled in the logic game playing, the algorithm will be deeply entrenched in their subconscious so it will facilitate their logical skill in later ages. Hopefully, the games can also enhanced their IQ like the Wff’n Proof game created by proessor Layman E. Allen in the Yale University.

Reblogged from https://integralisme.wordpress.com/2015/08/12/peircean-chips-game-of-logic/