Game of Life
John Horton ConwayConway was interested in a problem presented in the 1940s by mathematician John von Neumann, who attempted to find a hypothetical machine that could build copies of itself and succeeded when he found a mathematical model for such a machine with very complicated rules on a rectangular grid.
The Game of Life emerged as Conway's successful attempt to drastically simplify von Neumann's ideas. The game made its first public appearance in the October 1970 issue of Scientific American, in Martin Gardner's "Mathematical Games" column.
From a theoretical point of view, it is interesting because it has the power of a universal Turing machine: that is, anything that can be computed algorithmically can be computed within Conway's Game of Life.[2][3] Gardner wrote:
The game made Conway instantly famous, but it also opened up a whole new field of mathematical research, the field of cellular automata ... Because of Life's analogies with the rise, fall and alterations of a society of living organisms, it belongs to a growing class of what are called "simulation games" (games that resemble real life processes).The earliest interesting patterns in the Game of Life were discovered without the use of computers. The simplest static patterns ("still lifes") and repeating patterns ("oscillators"—a superset of still lifes) were discovered while tracking the fates of various small starting configurations using graph paper, blackboards, physical game boards (such as Go) and the like.
During this early research, Conway discovered that the R-pentomino
 failed to stabilize in a small number of generations. In fact, it takes
1103 generations to stabilize, by which time it has a population of 116
and has fired six escaping gliders
failed to stabilize in a small number of generations. In fact, it takes
1103 generations to stabilize, by which time it has a population of 116
and has fired six escaping gliders (these were the first gliders ever discovered)
(these were the first gliders ever discovered)Many different types of patterns occur in the Game of Life, including
- still lifes (block
 , ,
, ,
- oscillators (period 2 beacon
 , period 3 pulsar
, period 3 pulsar  , period 15 pentadecathlon
, period 15 pentadecathlon  ) and
) and - patterns that translate themselves across
the board called "spaceships" (glider
 , lightweight spaceship
, lightweight spaceship  ).
).
The prize was won in November of the same year by a team from the Massachusetts Institute of Technology, led by Bill Gosper; the "Gosper glider gun"
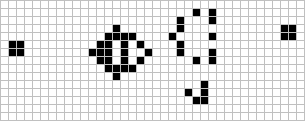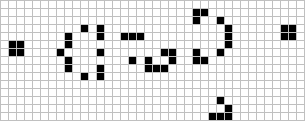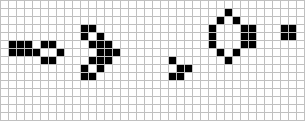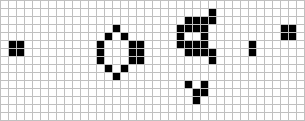
produces its first glider on the 15th generation, and another glider every 30th generation from then on. For many years this glider gun was the smallest one known.[19]
However, on April 28, 2015, Michael Simkin found a 36 cells Simkin glider gun

as the smallest glider gun ever found.
No comments:
Post a Comment